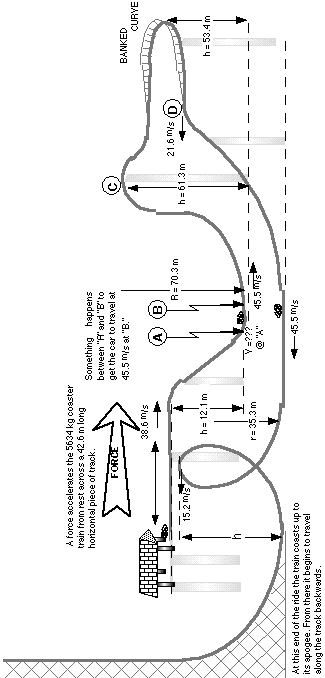
Using the information shown on the diagram on the other page,
determine the correct answers to the following questions.
1 How much force is used to accelerate the train across the first
42.6 m?
2 How many g's does the rider feel as he is pushed by the initial
accelerating force?
3 How fast is the car traveling at location A if it coasted
down the back side of the first hill?
4 At location B the incline is 90° of a circle. How many
g's does the rider feel as he enters the loop at location "B?"
5 How fast is the car traveling when it reaches location "C"?
6 In the banked turn the rider is traveling 21.6 m/s. What is the
optimum angle of the banked curve?
7 How many g's does the rider feel as he enters the loop?
8 What is the height of the loop?
9 If the radius at the top of the loop is 7.45 m, then how many g's
does the rider feel at this location?
10 How high does the coaster train coast at the end of the track?
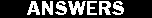
1 Use energy relationships to
solve
ET(BEGINNING) + WORK = ET(BEGINNING)
0 + Fd = (1/2) mv2
F(42.6) = (1/2) 5634)(38.6)2
F(42.6) = 4197217.32
F = 98,526.22817 N
F = 98,500 N
2 Use kinematics to
solve
vf2 = vo2 + 2ax
38.62 = 0 + 2a(42.6)
ac = 17.48779 m/s2
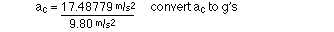
3 Use energy
relationships to solve
ET(AFTER FORCE) = ET (at A)
KE + PE = KE + PE
(1/2)mv2 + mgh =
(1/2)mv2 + 0
(1/2)v2 + gh =
(1/2)
v2 + 0
(1/2)(36.8)2 +
9.8(12.1) = (1/2)v2
863.56 = (1/2)v2
1727.12 = v2
v = 41.55863 m/s
v = 41.6 m/s
4 v = 45.5 m/s, r =
70.3 m

g's felt at the bottom = ac[in g's]
+ 1 g
g's felt at the bottom = 3.0049787 + 1 g
g's felt at the bottom = 4.00 g's
5 Use energy relationships and
compare locations "B" with "C"
ETB = ETC
KE + PE = KE + PE
(1/2)mv2 + 0 =
(1/2)mv2 + mgh
(1/2)v2 + 0 =
(1/2)v2 + gh
(1/2)(45.5)2 + 0 =
(1/2)v2 +
9.8(61.3)
1035.125 = (1/2)v2 +600.74
868.77 = v2
v = 29.4749 m/s
v = 29.5 m/s
6 Use banked curve
equations
v = 21.6 m/s, r = 42.3 m
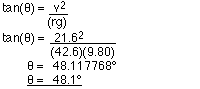
7 Use circular motion
equations
v = 45.5 m/s, r = 35.3 m 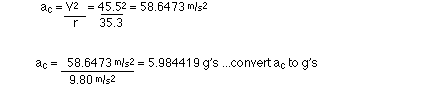
g's felt at the bottom = ac[in g's]
+ 1 g
g's felt at the bottom = 5.984419 + 1 g
g's felt at the bottom = 6.98 g's
8 Use energy
relationships
v(BOTTOM) = 45.5 m/s, V(TOP) = 15.2 m/s
ET(TOP) = ET(BOTTOM)
KE + PE = KE + PE
(1/2)mv2 + mgh =
(1/2)mv2 + 0
(1/2)v2 + gh =
(1/2)v2
(1/2)(15.2)2 +
(9.80)h = (1/2)(45.5)2
115.52 + 9.8(h) = 1035.125
h =93.8372 m
h = 93.8 m
9 Use circular motion
relationships
v = 15.2 m/s, r = 7.45 m
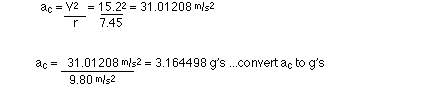
g's felt at the top of a loop = ac[in g's] + 1 g
g's felt at the top of a loop = 3.164498 + 1 g
g's felt at the top of a loop = 2.16 g's
10 Use energy relationships to
solve.
Velocity at the highest point will be zero, (apogee).
ET(BOTTOM) = ET(TOP)
KE + PE = KE + PE
(1/2)mv2 + 0 =
0 + mph
(1/2)v2 = gh
(1/2)(45.5)2 + =
(9.80)h
h =105.625 m
h = 106 m
If you use or find this page useful or have any
comments, please contact the author so maybe he'll do more.
Author: Tony Wayne
"ROLLER COASTER PHYSICS" TABLE
OF CONTENTS ... PHYSICS PAVILION TABLE OF
CONTENTS
<--PREVIOUS
SECTION ... NEXT SECTION -->