|
The information on this diagram is to be used for the accompanying
questions.
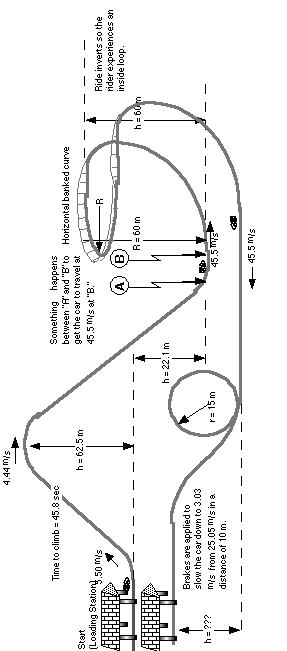
Using the information shown on the diagram on the other page,
determine the correct answers to the following questions.
1 How much power was used to pull the coaster car up the first hill?
(in watts and horsepower.)
2 How fast is the car traveling at location A if it coasted
down the back side of the first hill?
3 How many g's does the rider feel as he enters the bottom of the
next element if it's radius is 60.0 m, at location B?
4 How fast is the car traveling when it reaches the banked curve?
5 If the banked curve is at a 52.3° angle with the horizontal,
then what is the radius of the banked curve?
6 How many g's does the rider feel in the banked curve?
7 How many g's does a rider feel as he enters the bottom of the
loop?
8 How fast is the rider traveling at the top of the loop?
9 How many g's does the rider feel at the top of the loop?
10 As the car enters the station at the end of the ride, its brakes
are applied. How much power do the brakes exert on the car? (in watts
and horsepower.)
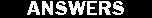
1 Use Energy relationships and
power to solve
vo = 5.50 m/s
vf = 4.44 m/s
h = 62.5 m
t = 45.8 s
m =6500 kg
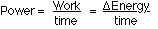
DET = [KEf + PEf] - [KEo +
PEo]
DET = [(1/2)m(vf)2 + mg(hf)]
- [(1/2)m(vo)2 + 0]
DET = [(1/2)(6500)(4.44)2 +
(6500)(9.80)(62.5)] - [(1/2)(6500)(5.50)2]
DET = 64069.2 + 3981250 - 98312.5
DET = 3947006.7 J
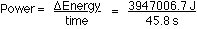
Power = 86,179.186 watts ...746 w = 1 hp
Power = 115.52 hp
2 Use Energy relationships
to solve
vo = 4.44 m/s ...at the hill
top
vf = ???? ...at the hill bottom
h = 62.5 + 22.1 = 84.6 m
ET @ the hill top = ET @ the hill bottom
KE + PE = KE + PE
(1/2)mv2 + mgh =
(1/2)mv2 + 0
(1/2)v2 + gh =
(1/2)v2 + 0
(1/2)(4.44)2 +
(9.80)(84.6) = (1/2)v2
838.94 = (1/2)v2
v = 40.96 m/s
3 Use circular motion
relationships to solve
v = 45.5 m/s, r = 60.0 m

g's felt at the bottom = ac[in gs]
+ 1 g
g's felt at the bottom = 3.52 + 1 g
g's felt at the bottom = 4.52 g's
4 Use Energy relationships to
solve
ET @ "B" = ET @ "A"
KE + PE = KE + PE
(1/2)mv2 + 0 =
(1/2)mv2 + mgh
(1/2)v2 = (1/2)v2 + gh
(1/2)(45.5)2 =
(1/2)v2+
(9.80)(60.0)
447.125 = (1/2)v2
v = 29.904 m/s
5 Use banked curves
v = 29.90401311 m/s ...from #4
q = 52.3°
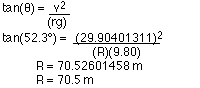
6 Use banked curves
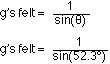
g's felt = 1.26
7 Use circular motion
relationships to solve
v = 45.5 m/s
...because it is at the same height as location "B."
r = 15 m
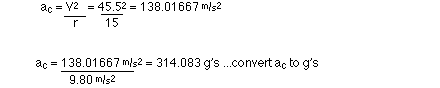
g's felt at the bottom = ac[in gs]
+ 1 g
g's felt at the bottom = 14.083 + 1 g
g's felt at the bottom = 15.0 g's
8 Use Energy relationships to
solve
ET @ bottom = ET @ top
KE + PE = KE + PE
(1/2)mv2 + 0 =
(1/2)mv2 + mgh
(1/2)v2 = (1/2)v2 + gh
(1/2)(45.5)2 =
(1/2)v2+
(9.80)(30.0)
741.125 = (1/2)v2
v = 38.5 m/s
9 Use circular motion relationships to solve
v = 38.5 m/s
...from #8
r = 15 m
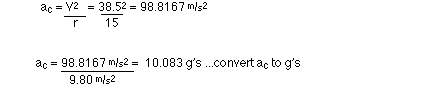
g's felt at the top = ac[in g's] -
1 g
g's felt at the top = 10.083 - 1 g
g's felt at the top = 9.08 g's
10 Use energy relationships and
power to solve
vo = 25.05 m/s
vf = 3.03 m/s
d = 10 m
t = 45.8 s
m =6500 kg
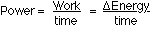
DET = [KEf + PEf] - [KEo +
PEo]
DET = [(1/2)m(vf)2 + 0] - [(1/2)m(vo)2 + 0]
DET = (1/2)(6500)(25.05)2 -
(1/2)(6500)(5.50)2
DET = 2010103.875J
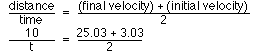
t = 0.712250712 s
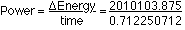
Power = 2822185.841watts ...746 w = 1 hp
Power = 3783.09 hp
If you use or find this page useful or have any
comments, please contact the author so maybe he'll do more.
Author: Tony Wayne
"ROLLER COASTER PHYSICS" TABLE
OF CONTENTS ... PHYSICS PAVILION TABLE OF
CONTENTS
<--PREVIOUS
SECTION ... NEXT SECTION -->
|