Intro to Design Example
This will show the reader the basic steps to designing a roller
coaster.
The example coaster will not be
the best possible design.
(I don't want students to use it as their own in other projects.)
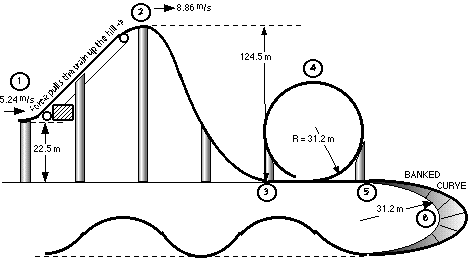
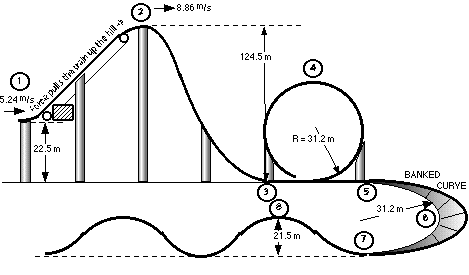
STEP 1 Draw a picture of what the coaster may look
like.
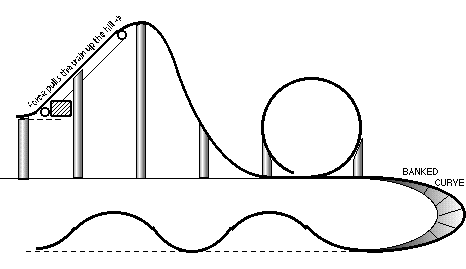
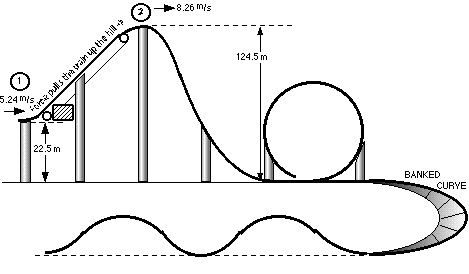
STEP 2 Assign some beginning numbers.
Numbers like the initial velocity as the coaster
train leaves the station. The mass of the coaster train. And/or an
initial velocity as it tops the first hill. (Label the pieces for
easy identification when analyzing.)
STEP 3 Begin to calculate everything you can and check to see
if it makes sense.
For this design start by calculating the force needed to pull the
train up the incline and the power to pull it up the incline.
In order to calculate the power force and power to pull it up the
incline I'm going to need the train's mass. So make up a reasonable
mass. This coaster is made up of 6 cars. Each car has a maximum mass,
with two riders at 100 kg each, of 735 kg; (535 kg car + 100 kg rider
+ 100 kg rider.) Therefore, the coaster train will have a mass of
4410 kg.
What angle will the first incline be? The designer can choose this
number too. 42° is good. The train is going to be pulled up
vertically a distance of, (124.5-22.5), 102.0 m.
|
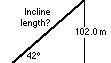
Incline length = 102/(sin42°)
Incline length = 152.4 m
ET(OUT OF STATION) + Work =
ET(TOP OF 1st HILL)
KE + PE +W = KE +PE
(1/2)mv2 + mgh + Fd =
(1/2)mv2 + mgh
(1/2)4410(5.24)2 +
4410(9.8)(22.5) + F(152.4) = (1/2)4410(8.26)2 +
4410(9.8)(124.5)
60544.008 + 972405 + F(152.4) = 150441.858
+ 5380641
F(152.4) = 4498133.85
F = 29515.314 N ... is the pulling force along the
incline.
How much time will it take to travel up the incline?
The acceleration of the train is found from
(vf)2 = (vo)2 +2ad
(8.26)2 = (5.24)2 + 2(a)d
a = 0.134 m/s2
vf = vo + at
8.26 = 5.24 + 0.134(t)
t = 22.537 sec ...is the time to climb the incline.
(Most initial lift times are between 60 and 120 seconds.)
It is beyond the scope of this book to show how to calculate the
time for each track element. It was shown here because of its ease of
calculation.
STEP 4 Calculate maximum velocity of the ride.
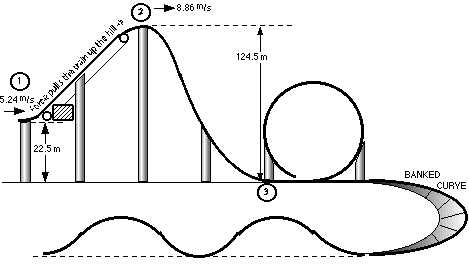
Since the 1st drop is the longest, the velocity at the bottom will be
the greatest, (location #3). Energy relationships will be used to
calculate the velocity.
ET(LOCATION #2) = ET(LOCATION #3)
KE + PE = KE +PE
(1/2)mv2 + mgh =
(1/2)mv2 + mgh
(1/2)4410(8.26)2 +
4410(9.8)(124.5) = (1/2)4410(v)2 +
4410(9.8)(0)
150441.858 + 5380641 =
2205(v)2
2508.428 = (v)2
v = 50.084
v = 50.1 m/s ... At the bottom of the first hill
That’s 112 mi/hr !!!
STEP 5 The loop.
For any loop, the designer would like to know the velocity as the
rider enters the loop; at the top of the loop; and as the rider
leaves the loop. The designer would also like to know the g’s
felt by the passengers. This is the location on the ride where riders
are most likely to pass out if the g’s are too much. The radius
in the loop below is made up.
The velocity as the rider enters the loop and as the rider leaves the
loop is the same as the velocity at the bottom of the first hill.
This is because all three locations are at the same height.
The velocity at the top of the loop is not the same as at the bottom.
As the coaster travels up the loop it will lose kinetic energy and
gain potential energy.
The height of the loop is simply double the radius. h = 2(31.2) =
62.4 m
ET(LOCATION #2) = ET(LOCATION #4)
KE + PE = KE +PE
(1/2)mv2 + mgh =
(1/2)mv2 + mgh
(1/2)4410(8.26)2 +
4410(9.8)(124.5) = (1/2)4410(v)2 +
4410(9.8)(62.4)
150441.858 + 5380641 =
2205(v)2 + 2696803.2
1285.388 = (v)2
v = 35.852
v = 35.9 m/s ... At the bottom of the first hill
That's 80.3 mi/hr !!!
If you are doing this calculation and you get an expression that
requires you to calculate the velocity by taking the SQUARE ROOT OF A
NEGATIVE NUMBER, then the loop is too tall for the given velocity at
the bottom of the loop. The velocity will need to be increased or the
height of the loop decreased.
To calculate the g's felt by the rider, calculate the centripetal
acceleration at each location, convert to g's and either add or
subtract a g as necessary.
As the rider enters and leaves the loop
v = 50.084 m/s
r = 31.2 m
ac = 8.2 g's
ac = 8.2 g's + 1g
ac = 9.2 g's ... That is an
incredible amount of g's. Most coasters do not go above 5 g's. To be
safe the radius at the bottom of the loop needs to be bigger.
As the rider passes the top of the loop
v = 35.852 m/s
r = 31.2 m
ac = 4.2 g's
ac = 4.2 g's - 1g
ac = 3.2 g's ... That is an
acceptable amount. But 3.2 g's is rather high for the top of a loop.
Most of the time the g's at the top of a loop are from 1.5 to 2
g's.
Because of the need for a larger radius as the rider enters the loop
above, this coaster might be a good candidate for an irregular loop
like the one below.
STEP 6 The banked curve.
The banked curve is a horizontal curve on the ground in this diagram.
Because it is at the lowest point it's velocity is equal to that of
location #3, where v = 50.084 m/s. For a first try
I'll make the radius 31.2 m.
The curve will be designed at the optimum angle where no friction or
outside lateral forces are needed to keep the car on the track at
speed. "At speed" means the velocity of the track design.
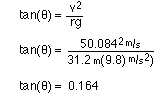
q = 9.3° .... That's almost a flat turn. It might be more
exciting to try to decrease the radius so a greater banking angle
will be needed.
The g's felt are calculated from
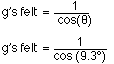
g's felt = 1.013 g's .... This is not much more than normal gravity.
These g's are the g's felt applied to your seat. Because this curve
is rather flat, it would be wise to examine lateral, centripetal,
acceleration in g's.
Lateral g's are the g's felt in the horizontal plain of the
curve.
v = 50.084 m/s
r = 31.2 m ... of the curve. This just happens to be the same as the
loop's radius.
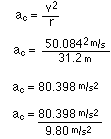
ac = 8.2 g's ... Do not add or
subtract a "g" because the circular motion is horizontal and not in
the vertical plain.
... That is a lot of lateral g's. That's 8.2 times the rider's
weight pressing him against the side of the coaster car. It is too
extreme. Maybe a value around 1 to 2 g's would be better tolerated by
the rider.
The banked curve needs to be redesigned.
STEP 7 The camel back
The camel back humps begin at the lowest part of the track and climb
to a height of 21.5 m. The calculations to check the velocity at the
top of the hump is similar to the one for the drop from location 2 to
3.
ET(LOCATION #7) = ET(LOCATION #8)
KE + PE = KE +PE
(1/2)mv2 + 0 =
(1/2)mv2 + mgh
(1/2)v2 + 0 =
(1/2)v2 + gh
(1/2)(50.084)2 + 0 =
(1/2)(v)2 +
(9.8)(21.5)
1254.203528 = (1/2)(v)2 +
210.7
2087.007056 = (v)2
v = 45.6838
v = 45.7 m/s ... At the bottom of the first camel back
hill.
That's 102 mi/hr !!!
It might be wise to decrease the height of the first drop to decrease
the velocity of the coaster as it enters the loop and the banked
curve. Then, redesign the loop and banked curve to reduce g's
experienced by the rider. As for the camel back humps at the end of
the ride, they probably need to either be taller or stretched out
horizontally. They are too narrow, horizontally, for 45.7 m/s.
If you use or find this page useful or have any
comments, please contact the author so maybe he'll do more.
Author: Tony Wayne
"ROLLER COASTER PHYSICS" TABLE
OF CONTENTS ... PHYSICS PAVILION TABLE OF
CONTENTS
<--PREVIOUS
SECTION ... NEXT SECTION
-->