FLUIDS Density and Pressure (know the definitions of density and pressure and the effect of depth on pressure in a fluid)

1. Write the definition of density here:

2. Write the definition of pressure here:

Consider the pressure at the bottom of the box of fluid shown in the figure.

3. Fill in the boxes to make “truth”

4.What happens to the pressure in a fluid as you double and triple the depth, h?

Archimedes’ Principle (know Archimedes’ principle and be able to apply it)

Fill a graduated cylinder with 60 ml (cm³) of water.

You will be submerging several shapes in the water.

5. What property of the shapes will determine how much water gets displaced?_______________________

6. According to Newton’s 3^rd, if the object pushes the water,______________________________________

This push from a fluid is called buoyant force.

7. The buoyant force of the water on the object equals the volume / mass / weight of water displaced. (Circle one word)

8. The quantity of water displaced equals the volume / mass / weight of the object. (Circle one word)

9.Zero the spring scale and then hang the first

object to measure its weight.

Submerge the object in the water (while still

hanging from the spring scale) and note

the water level in the graduated cylinder

and the new value on the spring scale.

The density of water is

1 gm/ml (1 gm/cm³) every

Cubic centimeter of water

displaced would have mass

of 1 gram and weight of

0.001 kg x 9.8 m/s².

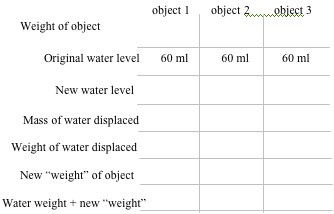
10. Did the apparent weight loss due to buoyant force equal the weight of water displaced?

11. Given a cube of volume 10 cm³ and mass 15 grams, what is its “weight” out of water? submerged in water?

12. Given a cube of volume 10 cm³ and mass 5.0 grams, what is its “weight” out of water? submerged in water?

13. What does it mean that the apparent weight in water was negative in #12?

14. How many ml of water would need to be displaced in #12 for the buoyant force to equal the weight?

15. How many ml of salt water (density 1.1 g/ml) need be displaced in #12 for buoyant force to equal the weight?

16. What would happen to an ocean liner so full that any more cargo would sink it, if it left the ocean and entered the

fresh water Great Lakes?

Many of the ideas in this worksheet were based on How Things Work by Louis Bloomfield

Pascal’s Principle: If you CHANGE the pressure of an ENCLOSED FLUID at one

location, it changes equally at all other locations in the fluid.

(know Pascal’s principle and be able to apply it)

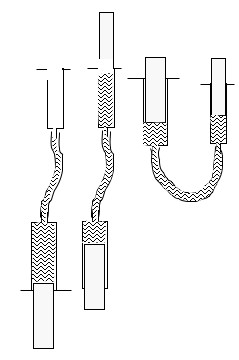
Select two syringes of differing diameters. Remove the plungers and

measure the inside diameter of each and enter it for 17 below.

Put the plunger all the way into the the larger syringe, attach a tube.

Put the tube into a container of water and draw back the plunger to fill the

tube and syringe with water.

Attach the smaller syringe (still without plunger) to the other end of the tube.

Hold the empty, plungerless syringe at the top with the water-filled tube and

larger syringe below so that any air bubbles rise to the top.

From the bottom, push the larger plunger up until the water rises to the top of

the smaller syringe.

Put the plunger back into the smaller syringe and press it down thus forcing

some water back into the larger plunger. There should be no air between

the two plungers. Put the two syringes into the holder.

17. Diameter of larger syringe_______________________

Diameter of smaller syringe _______________________

18. Cross-sectional area of larger syringe_________________

Cross-sectional area of smaller syringe______________________

19. If you pressed down on the larger syringe with a force of 10.0 newtons,

what increase in the pressure of the fluid should this cause? ________________________________

20. If that same pressure increase occurred in the smaller syringe, acting

on the smaller cross-sectional area of its plunger, what force should result?_____________________________

Place two spring scales on the two plungers, push on the larger plunger so that the spring scale reports a force of

10.0 N. MAINTAIN this 10 newtons throughout the activities that follow. The smaller plunger should start to rise. Observe carefully what the minimum force on the smaller plunger is that stops the rising. What is the minimum force that causes the smaller plunger to start going downward? Determine the minimum to stop the rise and to start the decent several times. Unfortunately, in addition to forces arising from your push and the pressure in the fluid, there is also pretty significant friction between the sides of the syringes and the plungers. When making the second plunger RISE, this friction would have REDUCED the force needed on the second spring scale to match the change in pressure. When making the second plunger DESCEND, the friction would have INCREASED the force on the second spring scale. Thus the averaging of the two values should remove the effect of the friction.

22. Comment on the results in the table above as regards Pascal’s Law.

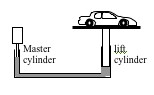
23. The hydraulic lift in an automobile garage is lifting a 20,000 N car. The piston

lifting the car has a radius of 5.5 cm. If the master cylinder has a radius of 0.48 cm,

what force must the motor at the master cylinder generate?

Bernoulli’s Principle (know Benoulli’s principle and be able to apply it)

24. Hold a strip of paper so that it curves and blow across the top of it.

It should move upward to some extent. Experiment with varying the

direction in which you blow and how hard you blow. What results in

the greatest “lift” for the paper?

25. Hold the paper so that it curves to the right or left instead of down as in 24. Blow again.

In what direction does the paper move?

Bernoulli’s Principle: As the speed of laminar flow across a surface increases, the pressure on the surface decreases

Laminar and Turbulent Flow

Laminar Flow: adjacent particles in the fluid move together

Turbulent Flow: adjacent particles move independently, chaotically

26. Crumple the paper up and then straighten it again and blow again across this wrinkled surface. Hopefully you will notice a decrease in the “lift”. Perhaps you will want to compare the wrinkled with a second smooth sheet. What do you think caused this decrease in lift?

27. Airplane wings use the Bernoulli effect as one of the sources of lift of for the airplane. What would be the effect of encountering a region of turbulent air (aka turbulence)?

28. You have been given a straw with its end bent down.

Tear off a small piece of paper and ball it up so that it will fit inside the straw. Place the paper

on a book and the bent end over the paper so that it is against the book. Now blow through the

long part of the straw and observe the paper. Explain why this occurred.

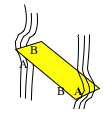
29. If you hold a card horizontally and drop it you might expect it to turn vertically

and slice through the air. However consider the air flow as it begins to tip as shown

in the picture. Will there be greater pressure at A or B? What effect will the

pressure differential have on the card’s orientation?

Bernoulli’s Principle is only true for laminar flow. With turbulent flow there is no pressure effect and air plane wings lose all of their lift.

(know the difference between laminar and turbulent flow, their consequences, and the factors that determine which will occur)

It is important for aeronautical engineers and many others to be able to predict when flows will cease to be laminar.

What follows are factors which affect how independently particles of a fluid move. When particles all move similarly the result is laminar flow. The more independently the particles move the greater the tendency for turbulent flow. For each of the factors you are to indicate whether they promote laminar or turbulent flow.

Viscosity of fluid, h; how attached one particle is to its neighbors.

30. Increasing h increases the probability of laminar / turbulent flow. (circle one word)

Velocity of fluid, v; how quickly one particle might be separated from its neighbors.

31. Increasing v increases the probability laminar / turbulent flow. (circle one word)

Density of fluid, r; as density increases it becomes less responsive to viscous forces

32. Increasing r increases the probability laminar / turbulent flow. (circle one word)

Size of impediments, ℓ: determines how far apart previously adjacent particles become

33. Increasing ℓ increases the probability laminar / turbulent flow. (circle one word)

Osborne Reynolds studied these effects near the beginning of the 20^th century and created the Reynolds Number, Re, for determining the conditions that will give rise to turbulent flow.

Turbulent flow commences when Re exceeds ABOUT 2300. (There is another transition in flow pattern at 100,000)

You are now going to look at laminar and turbulent flow in water.

You have been provided with a trough (section of gutter)

containing rheoscopic fluid (ground up fish scales

in water) which makes flow patterns visible. The inside

of your trough has been marked at 10 cm intervals.

Float a small piece of paper on the water near the middle of

the trough. As your partner gently lifts the trough up onto

two sticks, time the movement of the paper to get a sense of

the velocity with which the water is moving. Time the

movement again as the trough lifted off of the sticks so that

it is once again level. Repeat this 1 more time to get a

measure of the velocity at the middle of the trough when

these changes are made.

For water; viscosity,h is .001 Pa^.sec (Ns/m²) and density,r is 1000 kg/m³.

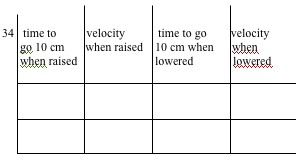
35. For the average of velocities you found above, how large an object could you place in the flow and not have turbulence? (That is Re < 2300)

36. Now, one by one, place the objects you’ve been given in the middle of the trough and see if laminar and turbulent flow occur as predicted. Comment on results.

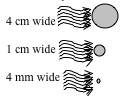
37. Turn the objects so that first the pointed and then the blunt ends face the flow. Comment on the results.

The hiss of water leaving a hose and the whoosh of objects moving through the air are noises caused by turbulence.

For air; density, r is 1.29 kg/m³ and viscosity, h is 1.83 x10^-5 Pa^.sec (Ns/m²)

Measure the dimensions of a meter stick. How fast would you need to move it through the air to cause turbulent flow? At that speed, how long would it take for the tip to travel 2 meters?

39. Comment on what you heard as you moved the stick slower and faster than the values from the table.

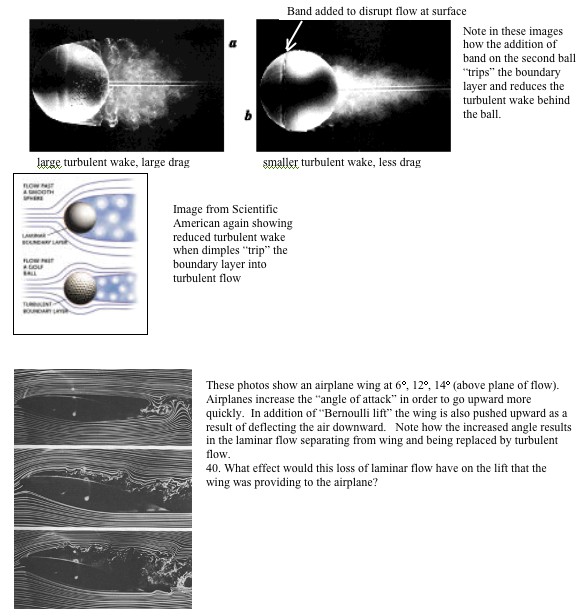
When the Reynolds number reaches 100,000 there is another transition in flow from the large turbulent wake that began at about 2300 to a very thin layer of turbulence right at the surface with laminar flow elsewhere. This loss of turbulent wake means a dramatic decrease in drag. Drag is the name given to retarding forces in a fluid. Without this effect baseballs would not be able to be hit for homeruns. It is also possible to achieve this boundary layer turbulence by “tripping the boundary layer.” The dimples on a golf ball and the fuzz on a tennis ball are designed to initiate turbulent flow at the surface and thus decrease the drag.

Band added to disrupt flow at surface