Energy with Hot Wheels
Presenter: Andy Jackson
Harrisonburg High School , ajackson[at symbol]harrisonburg.k12.va.us
Va. SOL:
PH.1 The student will plan and conduct investigations in which
- the components of a system are defined;
- instruments are selected and used to extend observations and measurements of mass, volume, temperature, heat exchange, energy transformations, motion, fields, and electric charge;
- information is recorded and presented in an organized format;
- metric units are used in all measurements and calculations;
- the limitations of the experimental apparatus and design are recognized;
- the limitations of measured quantities are recognized through the appropriate use of significant figures or error ranges;
- data gathered from non-SI instruments are incorporated through appropriate conversions; and
- appropriate technology including computers, graphing calculators, and probeware, is used for gathering and analyzing data and communicating results.
PH.2 The student will investigate and understand how to analyze and interpret data. Key concepts include
- a description of a physical problem is translated into a mathematical statement in order to find a solution;
PH.5 The student will investigate and understand the interrelationships among mass, distance, force, and time through mathematical and experimental processes. Key concepts include
- linear motion;
- uniform circular motion;
- projectile motion;
- Newton’s laws of motion;
- gravitation;
- planetary motion; and
- work, power, and energy.
PH.6 The student will investigate and understand that quantities including mass, energy, momentum, and charge are conserved. Key concepts include
- kinetic and potential energy;
Topic/Concept
Conservation of mechanical energy utilizing Hot Wheels track, cars, and radar gun
Materials
In lab
Safety Considerations
Excessive fun may result in playful recollection of childhood Hot Wheels experiences.
Presentation

Hot Wheels Radar Gun and G-Force track set are used for students to study conservation of mechanical energy and review vertical circular motion and projectile motion as a cumulative mechanics experience.
Hot Wheels
- Conservation of Mechanical Energy
A. Use the ring stands, clamps, and track to set up a hill like the one diagramed.
Use the ring stands, cross bars and books to make the track as stable as possible so that it does not sway when the car goes down the track.
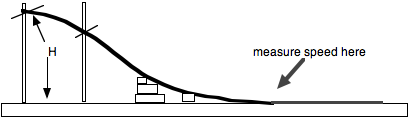
B. Now measure the height at the top of the hill (H).
C. Run the car and use the Hot Wheel’s Radar gun to measure the speed at the base of the hill. To use the radar gun
- put the settings in KPH and
- this puts the gun in Km/hr and a 1:64 scale setting
- aim the gun at the track so the car heads towards the gun
- pull the trigger, release the car. Hold the trigger until the car passes.
- release the trigger.
- The speed displayed is the highest speed the gun recorded.
- divide number by 64 to get actual speed in Km/hr
CALCULATION - AFTER ALL DATA COLLECTED
D. Use conservation of mechanical energy to calculate how fast the car should be going at the bottom of the hill. Calculate the relative error. Identify several sources of error.
I I. Conservation of Energy and projectile motion
A. Using the hill from part I add a ramp to the track. Measure the height at the end of the launching ramp.
Make sure and hold the ramp stable as the car goes down the track. By trial and error determine the maximum distance apart the ramps can be positioned.
CALCULATION - AFTER ALL DATA COLLECTED
B. Use some trigonometry to determine the angle at which the car will be launched. Use the measured speed at the bottom of the hill and conservation of energy to determine the speed the car will have when it leaves the launching ramp.
C. Use the projectile motion equations to determine the correct position of the landing ramp.
D. Evaluate the success of your calculations by calculating the relative error for the difference between the ramps. How many cm closer or farther apart do the ramps need to be to maximize the jump. Is this due to error or mistake?
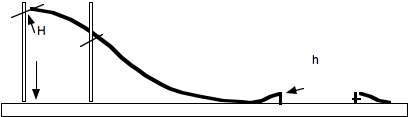
I I I. Conservation of Energy and a vertical loop
A. Replace the ramps with the vertical loop so the set up looks like this

B. Through trial and error determine the lowest height H the car can be released from so it just barely makes the vertical loop. The car should maintain contact with the track throughout the loop.
CALCULATION - AFTER ALL DATA COLLECTED
C. When the car is upside down at the top of the loop certain conditions must be met in order to make it around. The force diagram for the car at the top of the loop is this where W is the weight of the car and Fn is the normal force provided by the track. The two added together provide the centripetal force needed to keep the car in the circle. Just barely making it around the loop means touching the track with no force at the very top. Therefore the minimum conditions for a vertical loop are Fc = W. Use this fact and the radius of the loop to calculate the minimum speed at the top of the loop.
D. Use the height of the loop (h) and the minimum speed at the top of the loop to calculate the minimum height (H) from which the car must be released so it just makes it around the loop.
E. Evaluate the success of your calculations by calculating a relative error for H. How many cm higher or lower does the car need to be positioned to truly just barely make it around the loop? Is this due to error or mistake?
Teacher Tips Regarding Lab
This is such a fun way to experience conservation of energy and see mechanics at work. I use the radar gun in its scale model setting and then divide by 64. This makes a car going 10 Km/hr read as going 640 km/hr. Since the gun reads to the ones place in both cases, I’m able to get to the 1/10 km/hr by using the scale speed setting.
Sources & References
I found the radar gun for $20 and the G-Force track set for $12. Both are available at Wal-Mart, Target.com and other toy stores.
|