Ride Physiology Examples
EXAMPLE 1

SOLUTION
To calculate the g's at the top of the loop, you will need to know
the velocity of the rider there. To find velocity, use kinetic
energy.
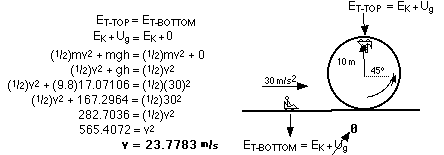
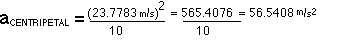
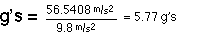
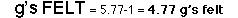
The rider will not pass out because 4.77 is less than 8
g's.
EXAMPLE 2

SOLUTION

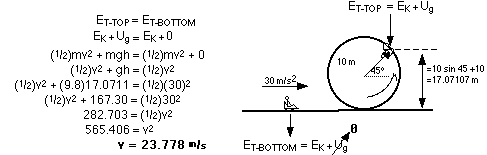
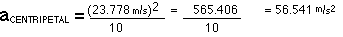
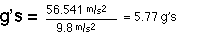
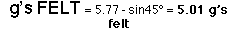
The rider will not pass out because 5.01 is less than 8
g's.
THE IRREGULAR LOOP
EXAMPLE
The simple loop is easy enough to calculate. The irregular shaped
loop needs a little more work. The velocity as the car enters the
loop should be known. First establish the g's felt at the bottom.
Subtract one g to know what the track exerts. Then convert these g's
to m/s2. Now solve for
the radius.
EXAMPLE
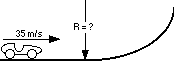
STEP 1 (I'm randomly choosing 6 g's as the limit for the
rider)
Therefore the centripetal acceleration of the track is
6g - 1g = 5gs.
STEP 2 (convert these g's to m/s2)
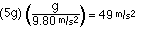
STEP 3
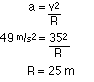
Now to calculate what the rider feels at the top of the loop.
Decide on the height of the loop. Then decide how many g's the rider
will experience. Use the loop formulae with centripetal acceleration
to calculate the radius.
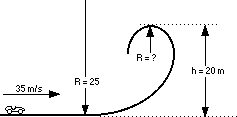
STEP 4
The top of the loop will be at 25 m. (Chosen pretty
much at random.)
STEP 5
I'm randomly choosing 6 g's again as the limit for the
rider. It could be almost any number. At the top of the loop add 1 g
for the centripetal force. ("Add" because the rider is upside down.)
6g's + 1 g = 7g
STEP 6 convert g's to m/s2
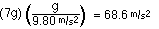
STEP 7
(1/2)(m)(35)2 = (1/2)(m)vo2 +(m)(9.80 m/s2)(20 m)
The m's divide out.
(1/2)(35)2 = (1/2)vo2 +(9.80 m/s2)(20 m)
vo = 28.86 m/s
STEP 8
Calculate the radius at the top
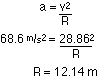
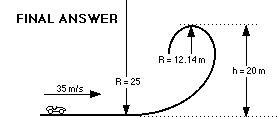

In reality, a person will not pass out the instant he/she reaches
8 g's. It will take a few seconds of being at 8 g's for the person to
pass out. But for the sake of easy calculations we will assume that
the instant 8 g's is reached a person will pass out. 8 g's is an
average. peaple generally pasout between 6 to 10 g's. (FYI: The 40 g
mark mentioned earlier is instantaneous for death.)
If you use or find this page useful or have any
comments, please contact the author so maybe he'll do more.
Author: Tony Wayne
"ROLLER COASTER PHYSICS" TABLE
OF CONTENTS ... PHYSICS PAVILION TABLE OF
CONTENTS
<--PREVIOUS
SECTION ... NEXT SECTION
-->