The Most Often Used Calculations

A roller coaster is called a coaster because once it starts it coasts through the entire track. No outside forces are required for most coasters. (A few have double or triple lift hills and braking sections.) Roller coasters trade height for velocity and velocity for height. Most all calculations rely on using velocity measurements in one way or another. The first step is being able to calculate the changes in speed.
In an ideal world, mechanical energy is conserved. Frictional forces are ignored in early design stages. (This document does not address the nuances of dealing with frictional forces.) Mechanical energy on a roller coaster comes in two basic forms. Kinetic energy, KE = (¹/2)mv², and potential energy, PE = mgh, due to gravity. Total energy, ET, is conserved and is equal to the sum of kinetic and potential at any single location.
ET = KE + PE (at any single location)

Calculation Algorithm to calculate a change in velocity associated with a change in height

Step 1 Identify two locations of interest. One with both a speed and a height and the other location with either speed or height.
Step 2 Write an equation setting the total energy at one location equal to the total energy at the other location.
Step 3 Solve for the unknown variable.

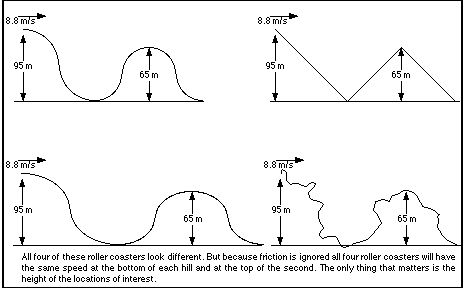
Example 1

What is the velocity at the bottom of the first hill?
Solution:
ET_(TOP) = ET_(BOTTOM)
KE + PE = KE +PE
(¹/2)mv² + mgh = (¹/2)mv² + mgh
(¹/2)v² + gh = (¹/2)mv² + mgh The masses cancel out because it is the same
coaster at the top and bottom.
(¹/2)v² + gh = (¹/2)v² + gh Substitute the numbers at each location
(¹/2)(8.8)² + 9.8(95) = (¹/2)v² + 9.8(0) The height at the bottom is zero because it is the lowest point when comparing to the starting height.
38.72 + 931 = (¹/2)v²
969.72 = (¹/2)v²
1939.44 = v²
v = 44.04 ^m/s ...at the bottom the the 1st hill.

Example 2

What is the velocity at the top of the second hill?
Solution:
ET_{(TOP OF 1}st _HILL) = ET_{(TOP OF 2}nd _HILL)
KE + PE = KE +PE
(¹/2)mv² + mgh = (¹/2)mv² + mgh
(¹/2)v² + gh = (¹/2)mv² + mgh The masses cancel out because it is the same coaster at the top and bottom.
(¹/2)v² + gh = (¹/2)v² + gh Substitute the numbers at each location
(¹/2)(8.8)² + 9.8(95) = (¹/2)v² + 9.8(65) Notice all the numbers on the left side come from the top
of the 1st hill while all the numbers on the right side come from the top of the 2nd hill.
38.72 + 931 = (¹/2)v² + 637

332.72 = (¹/2)v²
665.44 = v²
v = 25.80 ^m/s ...at the top the the 2nd hill.

This technique can be used to calculate the velocity anywhere along the coaster.