|
PROJECTILE MOTION AND ROLLER COASTER
HILLS
EXAMPLE CALCULATIONS 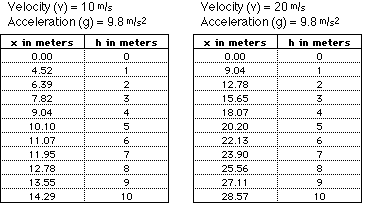
Catching the Rider For the bottom section of the track, the new equation has the desired outcome of changing the direction of the coaster from a downward motion to a purely horizontal motion. The track will need to apply a vertical component of velocity to reduce the coaster's vertical velocity to zero. The track will also need to increase the horizontal velocity of the coaster to the value determined from energy relationships. The velocity at the bottom of the hill is determined from which is This simplifies to where vB is the horizontal
velocity at the bottom of the hill. The value for vB will be used in later calculations.
substituting in our expression for "t" yields, where vxo is the horizontal velocity of the coaster at the transition angle and vyo is the vertical component of the velocity at the transition angle. "ay" is calculated from
Where "vy"is the final vertical velocity of zero, "vyo" is the vertical component of the velocity at the transition point, and "y" is the distance left to fall from the transition point to the ground. The horizontal velocity is determined from a parameter decided upon by the engineer. The engineer will want to limit the g forces experienced by the rider. This value will be the net g's felt by the rider. These net g's are the net acceleration. these values are plugged back into the original equation and x values are calculated as a function of y.
If you use or find this page useful or have any comments, please contact the author so maybe he'll do more. Author: Tony Wayne "ROLLER COASTER PHYSICS" TABLE OF CONTENTS ... PHYSICS PAVILION TABLE OF CONTENTS <--PREVIOUS SECTION ... NEXT SECTION --> |
A special thanks to VASTfor hosting our web site. |
||